$
\newcommand{\infdiv}{D\infdivx}
\newcommand{\comz}{\mathcal{Z}}
\newcommand{\vec}{\boldsymbol}
$
딥 러닝의 신뢰도를 개선하기 위한 모델 보정(calibration) 기법 소개
최근 다양한 분야에서 각광 받는 딥 러닝은 성능 면에서 매우 우수한 결과를 보여주고 있지만, 실제 애플리케이션에서 사용하기에는 신뢰성 측면에서 부족한 면이 있습니다. 대표적인 예로, 의료 영상에서 딥 러닝 모델을 사용해 질병 여부를 판단할 때 신뢰성에 대한 고려가 없다면 모델의 출력 결과인 예측 확률과 실제로 정답을 맞힐 확률이 일치하지 않는 문제가 있습니다. 다른 말로, 일반적인 딥 러닝 모델은 실제로 정답을 맞출 확률보다 자신이 예측한 결과를 과잉 확신하는 경향이 있습니다. 의료뿐만 아니라 자율주행, 금융 분야 등 중요한 판단을 해야 하는 실제 상황에서 위와 같이 예측한 확률은 높지만 틀린 판단(High-confidence errors)은 매우 치명적인 문제를 낳을 수 있습니다.
이런 상황을 해결하기 위해 모델 보정(Model calibration)이 필요합니다. 모델 보정은 딥 러닝 모델이 물체를 예측한 확률(Confidence score)과 실제로 정답을 맞출 정확도(Accuracy)가 일치하도록 조정을 해 줍니다. 개와 고양이를 분류하는 모델이 어떤 사진을 보고 고양이일 확률을 70%로 예측한다면 실제로 정답을 맞출 확률이 70%에 가까워야 보정이 잘 이뤄졌다고 말할 수 있습니다.
이러한 모델 보정은 예측 확률과 정확도의 관계를 나타내는 신뢰도 다이어그램(Reliability diagram)을 이용해서, 주어진 모델이 얼마나 잘 보정되어 있는지 쉽게 파악할 수 있습니다.
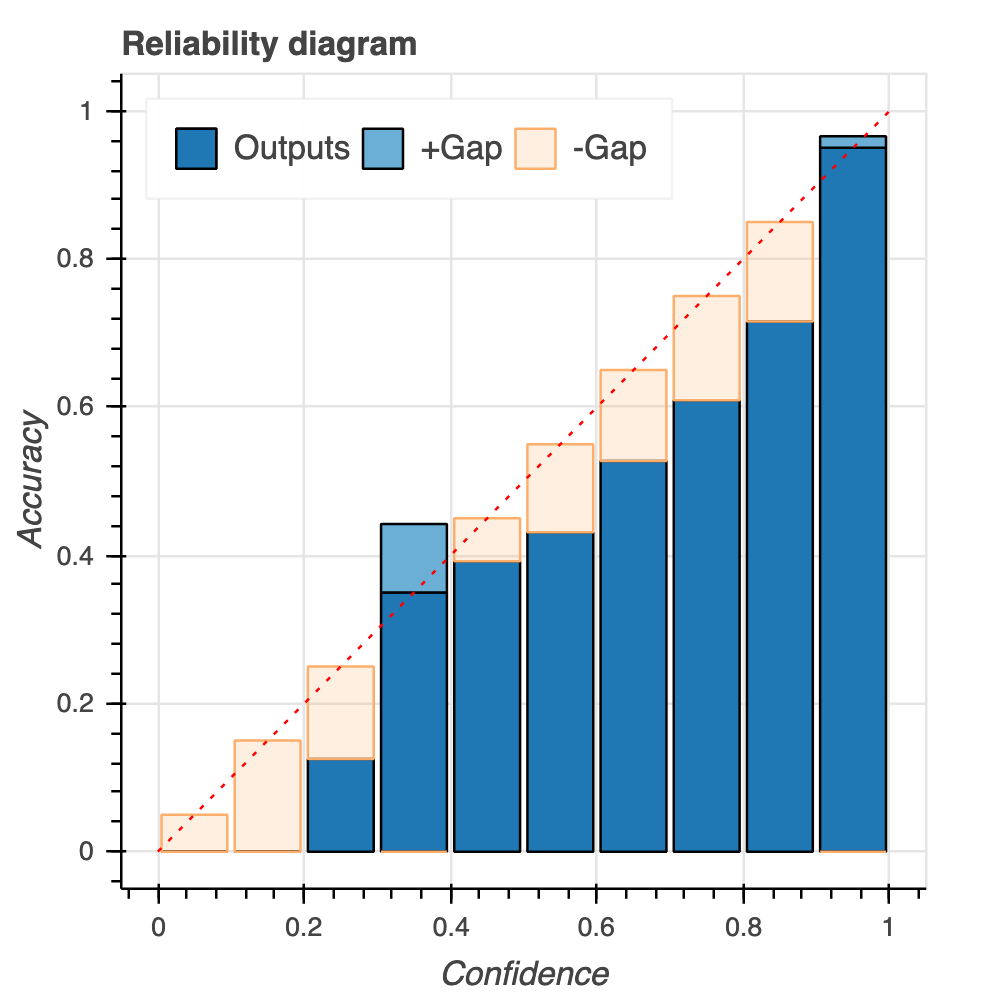
빨간 점선으로 된 대각선은 모델의 예측 확률과 정확도가 일치하는 이상적인 상태(완전 보정, Perfect calibration)를 보여줍니다. 이 빨간 점선보다 파란색 막대가 더 작다면, 실제 정확도보다 예측 확률이 큰 상태로 모델의 과잉확신(과대확신, over-confidence)을 의미합니다. 그 반대로 대각선 위로 막대 그래프가 넘어갈 경우, 정확도에 비해 낮은 확률로 예측을 한다고 볼 수 있고 이를 과소확신(under-confidence)이라고 부릅니다. 위에 나온 신뢰도 다이어그램은 예측 확률이 0.3-0.4, 0.9-1.0인 구간을 제외한다면 전반적으로 과잉확신 양상이 나타나는 모델이라고 해석할 수 있습니다.
이번 글에서는 이와 같은 딥 러닝 모델의 Miscalibration을 해소하는 기술 중 하나로 라벨 스무딩(Label Smoothing)에 대해서 알아보고자 합니다.
라벨 스무딩
딥 러닝에 대한 라벨 스무딩은 처음 Szegedy 논문에서 소개되었습니다.1
라벨 스무딩은 Hard label(One-hot encoded vector로 정답 인덱스는 1, 나머지는 0으로 구성)을 Soft label(라벨이 0과 1 사이의 값으로 구성)로 스무딩하는 것을 뜻합니다. $K$개의 클래스에 대해서, 스무딩 파라미터(Smoothing parameter)를 $\alpha$라고 할 때, $k$번째 클래스에 대해서 다음과 같이 스무딩을 합니다.
$$
\label{eq1}\tag{1}
y_k^{LS} = y_k(1-\alpha) + \alpha /K
$$
예를 들어, 클래스의 수가 5($K=5$)이고, 2 번째 클래스가 정답인 라벨에 대해서 다음과 같이 계산합니다($\alpha = 0.1$).
$$
y_2^{LS} = y_2(1-0.1) + \frac{0.1}{5}
$$
# Class number K = 5, 2nd class is ground-truth.
# y2_hard_label = [0, 1, 0, 0, 0]
# y2_soft_label = [0.02, 0.92, 0.02, 0.02, 0.02]
다시 말해, One-hot encoded vector에서 0인 값은 모두 0보다 큰 값인 0.02로, 정답을 나타내는 1은 1보다 작은 0.92로 라벨 스무딩을 통해 벡터값을 변환합니다. 이러한 변환을 다른 말로 label-smoothing regularization(LSR)이라고 부릅니다.

위 그림을 통해 라벨 스무딩 수식 \ref{eq1}을 일반적으로 생각해 보면, $\alpha/K$ 항은 정답을 제외한 다른 클래스를 균일 분포(Uniform distribution)로 만든다는 것을 알 수 있습니다.

한편 라벨 노이즈(Label noise)에 대해서도 라벨 스무딩 방법을 적용할 수 있는데, Ian GoodFellow는 Quora에 올라온 딥 뉴럴 네트워크 학습 시 어떻게 이상치(Outlier)를 처리할 것인지에 대한 질문에 다음과 같은 댓글을 달았습니다(Quora 참조).
Train using label smoothing. See “Rethinking the Inception architecture”. This is like incorporating a prior that there is label noise.
위에 나온 $y_k^{LS}$를 다시 생각해 보면, 결국 다른 클래스를 균일한 분포로 만들어서 라벨 노이즈를 사전 분포(Prior distribution)로 만든다는 것을 알 수 있습니다.
이렇게 스무딩된 소프트라벨을 크로스 엔트로피 함수에서 기존 라벨을 대체하여 사용합니다.
네트워크 마지막 레이어의 가중치(Weight)와 편향(Bias)을 $\omega_k$로, 입력값을 $\vec{x}$로 놓고, 모델이 $k$번째 클래스라고 예측할 가능도(Likelihood)인 $p_k$는 다음과 같습니다.
$$
p_k = \frac{e^{\vec{x}^T \omega_k} }{\sum_{l=1}^L e^{\vec{x}^T \omega_l} }
$$
이를 이용해 크로스 엔트로피(Cross-entropy) Loss를 최소화할 때 정답 타겟 $y_k$ 대신 $y_k^{LS}$를 사용하여 라벨 스무딩의 효과를 적용할 수 있습니다.
$$
H(\vec{y}, \vec{p}) = \sum_{k=1}^K -y_k^{LS}\log(p_k)
$$
이렇게 함으로써 최대 로짓이 다른 로짓보다 지나치게 커지는 것을 방지하고, 이는 딥 러닝 모델이 정답 타겟에 과잉 확신하는 현상을 해소해줍니다.
When Does Label Smoothing Help?2
이러한 라벨 스무딩의 효과를 좀 더 다층적으로 분석한 최근 논문을 하나 소개하고자 합니다.
구글 브레인(Google Brain)에서 발표한 위 논문에서는 라벨 스무딩이 네트워크 성능을 향상시키기 위해 범용적으로 사용되고 있지만, 라벨 스무딩을 왜, 언제 사용해야 하는지에 대해서는 잘 알려지지 않았다는 점을 지적하고 있습니다. 이 논문의 주요 시사점은 다음과 같습니다.
- 라벨 스무딩의 효과를 시각적으로 나타내기 위한 방법으로, 소프트맥스 출력을 위한 Fully-connected layer 이전인 네트워크 은닉층의 마지막 층(Penultimate layer)의 활성화를 이용해 시각화하는 방법을 소개합니다. 이런 시각화를 통해 라벨 스무딩의 유무에 따라 어떻게 표현성(Representation)이 달라지는지 확인할 수 있습니다.
- 라벨 스무딩이 모델 보정 방법의 하나인 만큼, 예측 확률(confidence)이 정확도에 잘 정렬된다는 것을 보여줍니다.
- Knowledge Distillation에 라벨 스무딩을 적용할 때, 라벨 스무딩으로 Teacher 모델을 학습하면 Student 모델의 성능이 오히려 악화됨을 보여줍니다. 이러한 원인으로 로짓의 정보 손실을 지적합니다.
Penultimate layer representations 시각화
먼저, 라벨 스무딩이 이미지 분류(Image classification)에서 어떤 효과를 낳는지 확인하기 위해 최종 은닉층의 활성화 값(penultimate layer activations)을 시각화하는 실험을 진행했습니다.
직관적으로 $k$ 번째 클래스에 대한 로짓(logit) $x^T w_k$은 이전 layer의 출력값(penultimate layer activation)인 $x$와 가중치 템플릿(weight template) $w_k$ 간의 squared Euclidean distance, ${\|x-w_k\|}^2 = x^T x - 2x^T+w^T_k w_k$로 생각할 수 있습니다. 여기서 $x^Tx$는 softmax 함수를 적용할 때 제거되고, $w^T_kw_k$는 모든 클래스에서 일반적으로 상수값을 가지기 때문에 무시할 수 있습니다. 이러한 의미에서 라벨 스무딩은 이전 레이어의 출력값과 정답 클래스의 템플릿이 최대한 가깝도록 만들고, 다른 클래스의 템플릿들에 대해서는 같은 거리로 떨어져 있도록 만드는 효과를 낳습니다.
이러한 라벨 스무딩의 특징을 관찰하기 위해 다음과 같은 시각화 방법을 제안했습니다.
- 데이터셋에서 3개 클래스를 선택한다.
- 이 세 개 클래스의 가중치 템플릿을 교차하는 평면의 직교 기저(Orthogonal basis)를 찾는다.
- 이 세 개 클래스로부터 뽑은 샘플 데이터의 최종 은닉층 활성화 값을 이 평면에 투영시킨다.
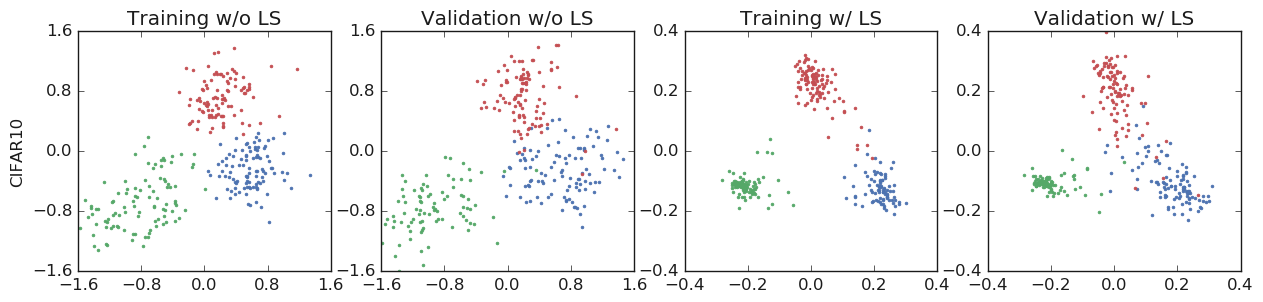
이와 같은 실험을 통해, 라벨 스무딩된 소프트 라벨로 네트워크를 학습했을 때 최종 은닉층의 활성화 값이 정답 클래스의 가중치 템플릿에 근접하고 정답이 아닌 클래스들의 가중치 템플릿에 대해 같은 거리만큼 멀어지도록 만드는 결과를 낳는다는 것을 확인할 수 있습니다.
라벨 스무딩의 효과를 측정 지표로 알아보기
두 번째로, 라벨 스무딩을 적용했을 때 모델 보정이 얼마나 효과적인지 보정 지표(ECE)와 신뢰도 다이어그램을 이용해 설명하고 있습니다. ECE는 Expected Calibration Error의 약자로써, 수식으로 다음과 같이 나타냅니다.
$$
\text{ECE} = \sum_{b=1}^B \frac{n_b}{N} | \text{acc}(b) - \text{conf}(b) |
$$
여기서, $N$은 전체 데이터 수, $n_b$는 해당하는 Bin에 속한 샘플의 갯수, $\text{acc}(b)$는 해당 Bin의 정확도를, $\text{conf}(b)$는 해당 Bin의 확신도를 각각 의미합니다.
서로 다른 데이터셋과 네트워크를 사용했을 경우 결과는 다음 표와 같이 정리할 수 있습니다.

Knowledge distillation에서의 (역)효과
라벨 스무딩이 항상 좋은 결과를 가져온다는 것은 아니라는 것을 지적하기 위해 Knowledge distillation(KD)에서의 실험을 통해 라벨 스무딩이 성능에 악영향을 줄 수도 있음을 확인했습니다. 무엇보다 라벨 스무딩이 Teacher 네트워크의 성능을 향상시켰을 때에도, 하드 라벨로 학습한 Teacher 네트워크와 비교할 때, 라벨 스무딩으로 학습된 Teacher 네트워크를 이용한 Student 네트워크는 오히려 성능이 떨어지는 걸 확인할 수 있습니다.

위 그림에서 KD에서 일반적으로 사용되는 Temperature Scaling (TS)를 사용한 Teacher 네트워크를 이용할 때는 베이스라인보다 성능을 향상시키지만, 라벨 스무딩을 이용한 Teacher 네트워크를 이용한 경우엔 베이스라인과 큰 성능 차이가 나지 않음을 확인할 수 있습니다.
이러한 결과를 낳는 원인은 Teacher 네트워크가 라벨 스무딩으로 학습될 때 로짓 사이의 상대적 정보가 '삭제'되기 때문입니다. 논문에서는 이런 정보 삭제를 Mutual Information(MI)으로 설명하고 있습니다.
어떤 두 개의 랜덤 변수가 있을 때, Mutual Information은 두 랜덤 변수가 얼마나 상호 의존하는지를 측정합니다. 또한 MI는 KL divergence로도 표현할 수 있습니다.
$$
I(X; Y) = H(X) - H(X|Y),
$$
또는
$$
I(X,Y) = D_{KL} (p_{XY} \Vert p_X \otimes p_Y).
$$
이 논문에서는 두 개의 랜덤 변수 $X$, $Y$를 각각, 학습 데이터셋 표본(Training example) 인덱스(Index)인 이산적 변수와 $K$개의 클래스로부터 선택된 두 개의 로짓 사이의 차이인 연속값으로 놓습니다.
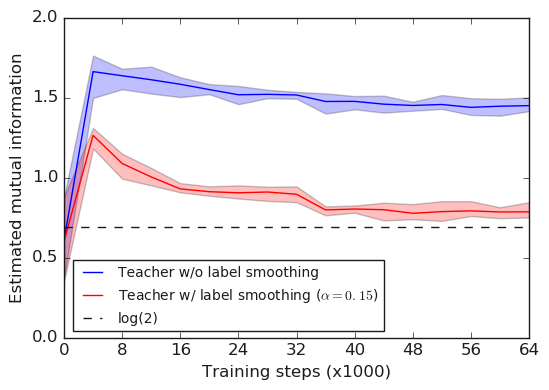
위 그래프를 보았을 때 전체적으로 라벨 스무딩을 사용하지 않았을 때 Mutual Information이 크고, Mutual Information이 큰 경우는 전체적인 클래스간의 유사도를 잘 나타내기 때문에 Knowledge Distillation에 적합한 반면, 라벨 스무딩은 Mutual Information을 줄이기 때문에 Knowledge Distillation에 부적합함을 알 수 있습니다.
마무리
지금까지 라벨 스무딩이라는 모델 보정 방법을 알아봤습니다. 하드 라벨을 소프트 라벨로 부드럽게 만들어서, 딥러닝 예측시 과잉확신을 줄여주는 라벨 스무딩은 매우 간결하면서도 딥러닝 모델에 쉽게 적용함으로써 모델의 예측 확률과 실제 정확도 간의 간극을 줄여주는 강력한 방법이라고 볼 수 있습니다. 이번 논문을 통해서 이미지 분류 모델에 대해서 클래스 간의 구분을 더 명확히 한다는 것을 시각적으로 잘 보여준 반면, Knowledge distillation처럼 정보 전달 모델에 대해서는 악영향을 줄 수도 있다는 것을 알 수 있었습니다.
내용을 요약하면 다음과 같습니다. 라벨 스무딩은
- ECE를 줄여서 모델 보정을 합니다.
- 분류 모델의 과잉확신을 해결합니다.
- 정보 삭제로 인해 Knowledge distillation에는 적합하지 않습니다.
- 내재적으로 모델의 예측을 보정함으로써 모델의 해석가능성(Interpretability)을 제공합니다.
모델의 신뢰도를 보장하는 기술은 앞으로 실제 애플리케이션에서 중요한 역할을 할 것으로 예상되며, 안전한 인공지능(AI Safety)을 위한 디딤돌이 될 수 있습니다. 다음 글에서는 적대적 공격(Adversarial attack)을 해결하는 방법으로 라벨 스무딩에 대해서 살펴볼 계획입니다.
References
- Guo et al., On Calibration of Modern Neural Networks, ICML 2017
- He et al., Bag of Tricks for Image Classification with Convolutional Neural Networks
[##최정렬##]
'Review' 카테고리의 다른 글
| 시간에 따른 도시 개발을 추적해봅시다 - SpaceNet 7 수상자 기술 분석 (0) | 2021.06.03 |
|---|---|
| Score-based Generative Modeling by Diffusion Process (4) | 2021.02.15 |
| Real-world Super-resolution via Kernel Estimation and Noise Injection (0) | 2020.07.15 |
| Anomaly detection using one class neural networks (Raghavendra Chalapath, 2018) (1) | 2020.07.03 |
| CVPR 2020 동향 분석 (0) | 2020.06.19 |




